Linear algebra with applications by otto bretscher 5th edition – Linear Algebra with Applications by Otto Bretscher, 5th Edition, is a comprehensive and accessible introduction to linear algebra, providing a solid foundation for students in various fields. With its clear explanations, engaging examples, and numerous applications, this book offers a deep understanding of the subject matter.
Linear algebra is a branch of mathematics that deals with vector spaces, matrices, and linear transformations. It has widespread applications in computer graphics, physics, engineering, economics, and many other disciplines. Bretscher’s book provides a thorough exploration of these concepts, making it an invaluable resource for students seeking to master linear algebra.
1. Introduction to Linear Algebra with Applications by Otto Bretscher 5th Edition
Linear Algebra with Applications by Otto Bretscher is a comprehensive textbook designed for undergraduate students in mathematics, science, and engineering. It provides a thorough introduction to the fundamental concepts of linear algebra and their applications in various fields.
The book is written in a clear and concise style, with numerous examples and exercises to reinforce understanding. It covers a wide range of topics, including:
- Vectors and matrices
- Systems of linear equations
- Vector spaces and subspaces
- Matrices and matrix operations
- Determinants and eigenvalues
- Applications of linear algebra
Linear Algebra with Applications is an essential resource for students who want to develop a strong foundation in linear algebra and its applications.
2. Key Concepts and Terminology

Linear algebra is the study of vectors and matrices. Vectors are ordered lists of numbers, and matrices are rectangular arrays of numbers. Linear algebra has many applications in fields such as computer graphics, physics, and economics.
Some of the key concepts in linear algebra include:
- Vectors: Vectors are mathematical objects that have both magnitude and direction. They can be represented as ordered lists of numbers, such as (1, 2, 3). Vectors can be added, subtracted, and multiplied by scalars.
- Matrices: Matrices are rectangular arrays of numbers. They can be used to represent systems of linear equations, transformations, and other mathematical objects. Matrices can be added, subtracted, and multiplied by other matrices or by scalars.
- Linear transformations: Linear transformations are functions that map vectors to vectors. They can be represented by matrices. Linear transformations can be used to rotate, scale, and shear vectors.
These are just a few of the key concepts in linear algebra. For a more detailed introduction, see the textbook Linear Algebra with Applications by Otto Bretscher.
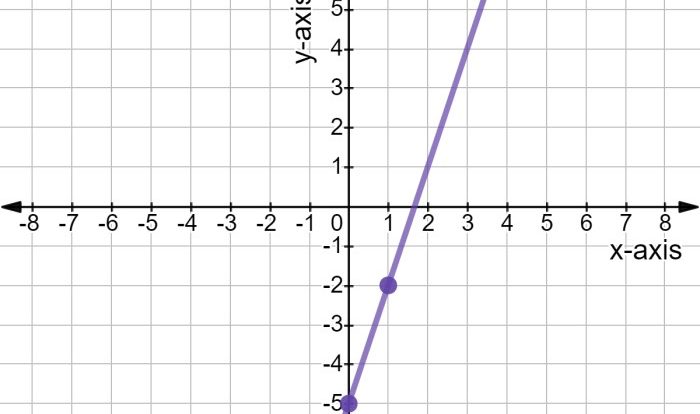
3. Systems of Linear Equations

A system of linear equations is a set of equations that can be written in the form Ax = b, where A is a matrix, x is a vector of unknowns, and b is a vector of constants. Systems of linear equations can be solved using a variety of methods, including Gaussian elimination, Cramer’s rule, and matrix inversion.
Gaussian elimination is a method for solving systems of linear equations by transforming the matrix A into an upper triangular matrix. Cramer’s rule is a method for solving systems of linear equations by computing the determinant of the matrix A and the determinants of the matrices obtained by replacing each column of A with the vector b.
Matrix inversion is a method for solving systems of linear equations by computing the inverse of the matrix A.
Systems of linear equations have many applications in fields such as computer graphics, physics, and economics. For example, systems of linear equations can be used to solve for the coefficients of a polynomial, to find the equilibrium prices of a market, and to compute the forces acting on a rigid body.
4. Vector Spaces and Subspaces
A vector space is a set of vectors that can be added, subtracted, and multiplied by scalars. Vector spaces have many applications in fields such as computer graphics, physics, and economics.
Some of the key concepts in vector spaces include:
- Linear combinations: A linear combination of vectors is a sum of the vectors multiplied by scalars. Linear combinations can be used to represent vectors as points in space.
- Span: The span of a set of vectors is the set of all linear combinations of the vectors. The span of a set of vectors is a subspace of the vector space.
- Linear independence: A set of vectors is linearly independent if no vector in the set can be written as a linear combination of the other vectors. Linearly independent sets of vectors can be used to form bases for vector spaces.
Vector spaces and subspaces are important concepts in linear algebra. They are used to represent a wide variety of mathematical objects, such as points in space, forces, and polynomials.
5. Matrices and Matrix Operations
A matrix is a rectangular array of numbers. Matrices can be used to represent systems of linear equations, transformations, and other mathematical objects. Matrices can be added, subtracted, and multiplied by other matrices or by scalars.
Some of the key types of matrices include:
- Square matrices: Square matrices are matrices with the same number of rows and columns. Square matrices can be used to represent transformations of the plane.
- Diagonal matrices: Diagonal matrices are square matrices with all off-diagonal elements equal to zero. Diagonal matrices can be used to represent scalings and rotations of the plane.
- Invertible matrices: Invertible matrices are square matrices that have an inverse. Invertible matrices can be used to solve systems of linear equations.
Matrix operations are used to combine and manipulate matrices. Some of the most common matrix operations include:
- Addition and subtraction: Matrices can be added and subtracted if they have the same dimensions. The resulting matrix is the matrix obtained by adding or subtracting the corresponding elements of the two matrices.
- Multiplication: Matrices can be multiplied by other matrices or by scalars. The resulting matrix is the matrix obtained by multiplying each element of the first matrix by the corresponding element of the second matrix or by the scalar.
- Transposition: The transpose of a matrix is the matrix obtained by interchanging the rows and columns of the matrix.
Matrices and matrix operations are essential tools for linear algebra. They are used to solve systems of linear equations, to represent transformations of the plane, and to compute the eigenvalues and eigenvectors of a matrix.
6. Determinants and Eigenvalues
The determinant of a square matrix is a number that is associated with the matrix. The determinant can be used to determine whether a matrix is invertible. The determinant is also used to compute the area of a parallelogram and the volume of a parallelepiped.
Eigenvalues and eigenvectors are special vectors and scalars that are associated with a square matrix. Eigenvalues are the scalars that, when multiplied by the corresponding eigenvectors, produce a vector that is parallel to the eigenvector. Eigenvalues and eigenvectors are used to analyze the behavior of linear transformations.
Determinants and eigenvalues are important concepts in linear algebra. They are used to solve systems of linear equations, to represent transformations of the plane, and to compute the eigenvalues and eigenvectors of a matrix.
7. Applications of Linear Algebra
Linear algebra has many applications in fields such as computer graphics, physics, and economics. Some of the most common applications of linear algebra include:
- Computer graphics: Linear algebra is used to represent and manipulate 3D objects in computer graphics. Linear algebra is also used to create special effects, such as lighting and shading.
- Physics: Linear algebra is used to solve problems in physics, such as the motion of objects and the flow of fluids. Linear algebra is also used to represent and manipulate tensors, which are mathematical objects that are used to describe the physical properties of materials.
- Economics: Linear algebra is used to solve problems in economics, such as the allocation of resources and the pricing of goods and services. Linear algebra is also used to represent and manipulate matrices, which are used to represent economic data.
These are just a few of the many applications of linear algebra. Linear algebra is a powerful tool that can be used to solve problems in a wide variety of fields.
Questions Often Asked
What are the key features of Linear Algebra with Applications by Otto Bretscher, 5th Edition?
Key features include clear explanations, engaging examples, numerous applications, and a focus on developing a deep understanding of linear algebra.
Who is the intended audience for this book?
This book is suitable for undergraduate students in mathematics, computer science, engineering, and other disciplines seeking a comprehensive introduction to linear algebra.
What are some of the applications of linear algebra covered in the book?
Applications include computer graphics, physics, engineering, economics, and many other areas where linear algebra plays a crucial role.