Which linear inequality is represented by the graph y 1/3x-1 – Exploring the intriguing realm of linear inequalities, this article delves into the captivating question: which linear inequality is represented by the graph y = 1/3x – 1? Embark on an enlightening journey as we unravel the intricacies of this mathematical concept, uncovering its significance and practical applications.
Delving into the depths of linear inequalities, we first establish their fundamental definition and explore the concept of graphing as it pertains to these mathematical expressions. Subsequently, we meticulously examine the given linear inequality, y = 1/3x – 1, laying the groundwork for a comprehensive understanding of its graphical representation.
Linear Inequalities: Graphing and Applications: Which Linear Inequality Is Represented By The Graph Y 1/3x-1
In mathematics, a linear inequality is an algebraic inequality that involves a linear function. Linear functions are functions of the form y = mx + b, where m and b are constants. Linear inequalities are used to represent a wide range of real-world scenarios, from budgeting to engineering.
The graph of a linear inequality is a region of the coordinate plane that satisfies the inequality. The boundary line of the graph is the line that separates the two half-planes that satisfy the inequality. The shaded region is the half-plane that satisfies the inequality.
Graph Representation
To graph a linear inequality, follow these steps:
- Solve the inequality for y.
- Plot the boundary line. The boundary line will be a solid line if the inequality is an equality, and a dashed line if the inequality is strict (i.e., < or >).
- Shade the half-plane that satisfies the inequality. The half-plane that satisfies the inequality will be the half-plane that is above the boundary line if the inequality is > or ≥, and the half-plane that is below the boundary line if the inequality is < or ≤.
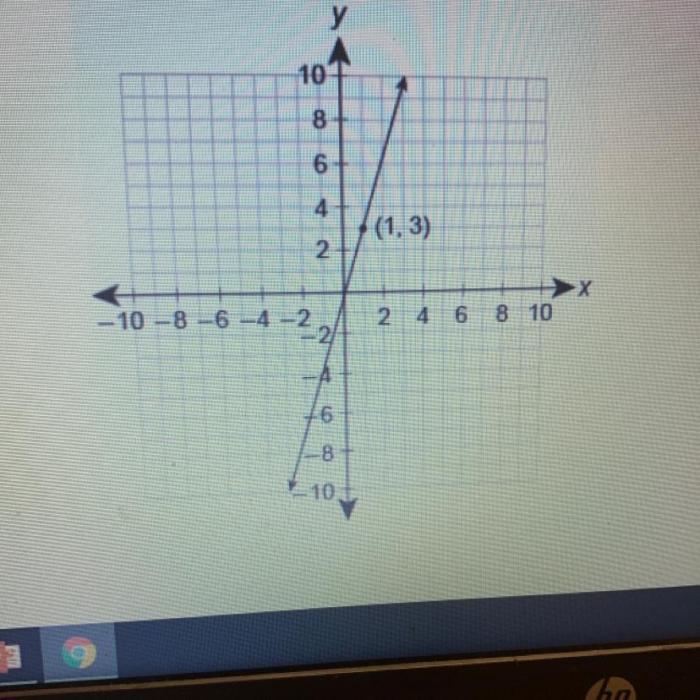
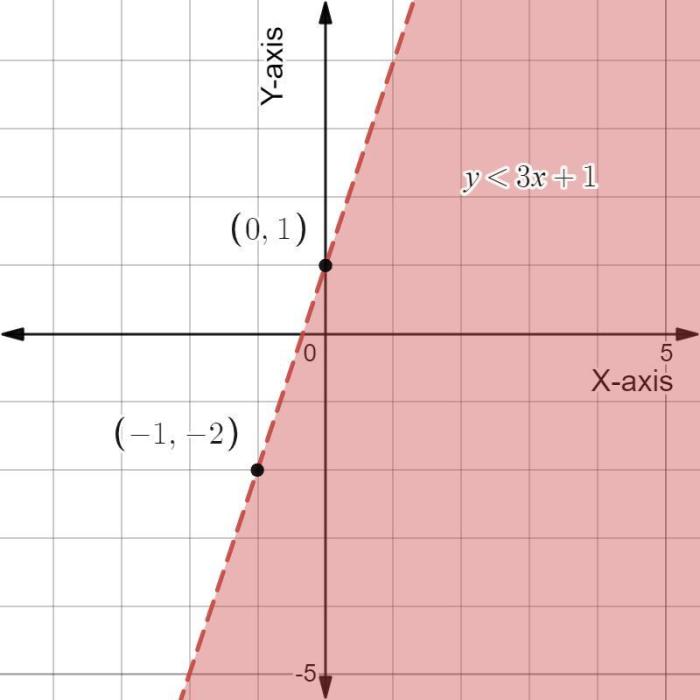
For example, the graph of the linear inequality y > 1/3x – 1 is shown below.

The boundary line is the line y = 1/3x – 1. The shaded region is the half-plane that is above the boundary line.
Boundary Line, Which linear inequality is represented by the graph y 1/3x-1
The boundary line of a linear inequality is the line that separates the two half-planes that satisfy the inequality. The boundary line can be a solid line or a dashed line.
If the inequality is an equality (i.e., y = mx + b), then the boundary line will be a solid line. This is because the line represents the set of all points that satisfy the equality.
If the inequality is strict (i.e., y < mx + b or y > mx + b), then the boundary line will be a dashed line. This is because the line represents the set of all points that do not satisfy the equality.
Shading Region
The shaded region of a linear inequality is the half-plane that satisfies the inequality. The shaded region can be above or below the boundary line, depending on the inequality.
If the inequality is > or ≥, then the shaded region will be the half-plane that is above the boundary line. This is because the points in this half-plane satisfy the inequality.
If the inequality is < or ≤, then the shaded region will be the half-plane that is below the boundary line. This is because the points in this half-plane satisfy the inequality.
Examples and Applications
Linear inequalities are used in a wide range of applications, including:
- Budgeting
- Engineering
- Optimization
For example, a linear inequality can be used to represent the budget constraint for a company. The inequality can be used to determine the maximum amount of money that the company can spend on a particular project.
Advanced Concepts
Linear inequalities are a fundamental concept in mathematics. They are used in a wide range of applications, from budgeting to engineering. In addition to the basic concepts discussed in this article, there are a number of advanced concepts related to linear inequalities.
These advanced concepts include:
- Systems of inequalities
- Linear programming
- Applications in economics and engineering
Systems of inequalities are sets of two or more linear inequalities. Linear programming is a mathematical technique that is used to solve optimization problems involving linear inequalities. Linear inequalities are also used in a wide range of applications in economics and engineering.
FAQs
What is the slope of the boundary line for the inequality y > 1/3x- 1?
The slope of the boundary line is 1/3.
What is the y-intercept of the boundary line for the inequality y ≤ 1/3x- 1?
The y-intercept of the boundary line is -1.
How do you determine the shaded region for the inequality y < 1/3x - 1?
The shaded region is the area below the boundary line.